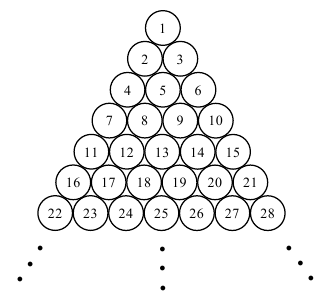
دو فرد A و B در پازلی به شکل زیر قرار گرفته اند که شامل تعداد نامحدودی دایره هایی که به یک اندازه هستند می باشد. این دو نفر در ابتدا بروی دو دایره (نه الزاما دو دایره مجزا) قرار گرفته اند . فرد A می خواهد به نزد فرد B برود. در هر مرحله او فقط می تواند از روی دایره ای که روی آن قرار گرفته است به یکی از دایره های مجاور حرکت کند. دو دایره مجاور هم آنهایی هستند که در یک نقطه مشترک باشند.
الگوریتمی بنویسد که شماره دو دایره ای را که در ابتدا این دو نفر روی آن قرار گرفته اند را به عنوان ورودی دریافت کرده و حداقل تعداد مراحلی را که فرد A برای رسیدن به فرد B نیاز دارد را پیدا کند
1) یک رکورد سه بخشی در نظر می گیریم :
[تعداد مراحل پیموده شده] - count
[موقعیت هایی (شماره دایره هایی) که در مراحل قبل در آنها بودیم] - prev
[موقعیتی (شماره دایره ای) که در آن هستیم] - loc
2) متغیر min که کمترین تعداد مراحل لازم است را روی مقدار بزرگی مثل 10000 تنظیم می کنیم.
3) با توجه به رکورد تعریف شده، به ترتیب مقادیر 0 مرحله (عدد 0) و موقعیت فرد A (شماره دایره ای که A در آن
قرار دارد) و مجددا موقعیت فرد A (موقعیت فعلی) را در پشته قرار می دهیم.
4) اگر پشته خالی است، عملیات خاتمه یافته و مقدار min حداقل تعداد مراحل لازم است، اگر همچنان 10000 است
بدان معنا است که هیچ راهی برای رسیدن به B وجود نداشته است.
5) مقادیر رکورد را از پشته می خوانیم و در loc و prev و count قرار می دهیم.
6) اگر loc برابر شماره دایره ای است که B در آن قرار دارد، یک مسیر برای رسیدن به B یافته ایم، تعداد مراحل یعنی
count را با min مقایسه می کنیم. اگر count کوچکتر بود مقدار اش را در min کپی می کنیم. در هر صورت
جستجوی این مسیر تمام شده و به مرحله 4 باز می گردیم.
7) هنوز به B نرسیده ایم، مقدار count را یک واحد افزایش می دهیم تا برای رفتن به دایره دیگری آماده شویم.
8) بررسی می کنیم که دایره هایی که با دایره فعلی (loc) نقطه مشترک دارند کدام ها هستند. در مورد هر کدام شان
بجز آنهایی که در prev هستند (که قبلا در آنها بودیم، نمی خواهیم به عقب بر گردیم یا حلقه بسازیم)، به ترتیب
مقادیر زیر را مطابق رکورد در پشته قرار می دهیم (برای هر دایره مجاور یک رکورد جدید در پشته قرار می دهیم) :
مقدار count
مقدار قبلی prev به همراه مقدار فعلی loc
موقعیت دایره مجاور (شماره دایره ای که مجاور است و در prev هم وجود ندارد)
9) به مرحله 4 باز می گردیم
این الگوریتم پیشروی و عقب نشینی دارد. هر بار که به دایره ای برسد که چندین دایره مرتبط دارد، موقعیت شان
را به خاطر می سپارد (پشته) و یکی از این دایره ها را دنبال می کند. هر بار که آن مسیر به پایان رسید، مجددا
به پشته رجوع می کند تا یک مسیر دیگری که در خاطر داشته پیگیری کند. زمانی که پشته خالی شد تمامی
مسیر های ممکن امتحان شده اند.